Vertexing Algorithms with the ATLAS Experiment (SULI) Strong Cosmic Censorship (Part III Essay) Invisible Higgs decays (BLUR) Massive electrodynamics (honors thesis)

Strong Cosmic Censorship in Asymptotically de Sitter Spacetimes

Part III Essay, University of Cambridge (January 2019–April 2019).

Essay Setter: Jorge Santos, DAMTP, University of Cambridge

Part of the Penrose diagram of the Reissner-Nordström black hole in asymptotically flat space. As they approach the Cauchy horizon \(\mathcal{CH}^+\), an observer B in the interior (region II) sees light pulses from the exterior (region I) as infinitely blueshifted. This effect produces a singular energy density before B can actually reach the Cauchy horizon.

Introduction

The strong cosmic censorship conjecture, originally formulated by Roger Penrose, is a statement about the limitations of classical general relativity. Stated simply, this conjecture asserts that physically reasonable spacetimes are globally hyperbolic, i.e. they admit an initial value (Cauchy) surface on which suitable initial conditions can be specified so that a unique solution consistent with the Einstein equations can be constructed for the entire spacetime manifold. At heart, the conjecture is motivated by questions of the predictive power of the Einstein equations, considered as an initial value problem. Does the deterministic nature of the Einstein equations ever break down? Strong cosmic censorship requires that the answer to this question is "generically, no."

Motivation

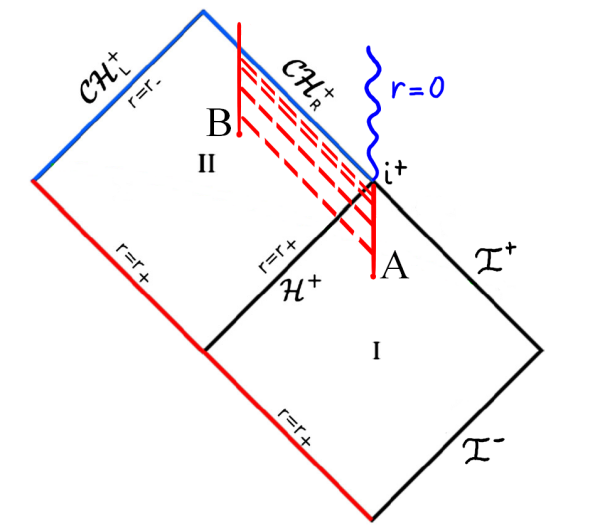
In the first place, determining the correct mathematical language for strong cosmic censorship is a challenging task. In the study of classical gravity, it is well-known that specific spacetimes which are not globally hyperbolic exist, such as the Reissner-Nordström and Kerr-Newman spacetimes. However, strong cosmic censorship suggests that there is a characteristic instability in these spacetimes which means that realistic spacetimes (i.e. ones subject to perturbation) are expected to be globally hyperbolic. Making this statement precise is one focus of current research.

Moreover, the aforementioned instability is known to be weaker in spacetimes with a positive cosmological constant, the so-called asymptotically de Sitter spacetimes. Studying strong cosmic censorship in these spacetimes may give us more insight into the mathematical nature and limitations of the Einstein equations.

Tasks and Skills

For this project, I was responsible for reading several key articles of the contemporary literature on strong cosmic censorship and synthesizing their content into a single 5000–8000 word essay. I typeset the essay in \(\LaTeX\) and designed original figures to supplement my discussion. In the essay, I analyzed the behavior of solutions to the wave equation in curved spacetime and studied the smoothness of such solutions near the Cauchy horizon. I then rederived analytic results about the characteristic decays of these solutions and compared these results to numerical simulations. By performing this analysis, I argued that the strong cosmic censorship conjecture may be violated in the asymptotically de Sitter Reissner-Nordström spacetime when the background spacetime is strongly curved and the black hole is sufficiently charged.

Results and Broader Impacts

In my essay, I discuss several different formulations of the strong cosmic censorship conjecture and justify why the modern formulation as posed by Christdoulou is most in the spirit of Penrose's orignal conjecture. I then provide a pedagogical introduction to the quasinormal modes, a key tool in the study of perturbations to black hole spacetimes. I motivate the crucial result that knowing the decay of quasinormal modes near the event horizon of a black hole is in fact sufficient to establish a violation of strong cosmic censorship. Finally, I characterize the parameter space of both the Reissner-Nordström-de Sitter (RNdS) and Kerr-de Sitter solutions in terms of the quasinormal modes and show that while the near-extremal RNdS solutions do violate all smooth formulations of cosmic censorship, no such violations are observed in the much more astrophysically relevant Kerr-de Sitter solutions.

Documentation